Consider a function f ( x ) which has the following graph:

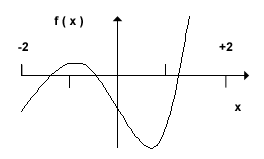
We can see that the value of  f ( x ) becomes zero at three different values of x. One of them is  between -2 and -1, the next is  between -1 and zero, and the third one is  between +1 and +2.  These values of x are called the roots of the function f(x).  Root finding is usually an iterative procedure, which starts with an estimate of the root and produces better approximations.

 Our challenge in root finding is to locate the root with a prescribed precision. How do we specify precision? There are two different ways of doing so, and sometimes we may want to have both of them used in a specific problem.

 The smallness of f(x) test: If at one point of our iteration the absolute value of the function f(x) drops below a prescribed tolerance then we can stop the iteration and say that we have a good approximation to the root.  For example, in the function illustrated in the graph if we have | f ( x_n ) | < 0.001 * | f ( 0 ) | we can say that x_n is a very reasonable estimate of the root. Note that we must have a relative measure of smallness.

 The other way of specifying precision is the closeness of successive approximations test : If at some stage of our iteration the absolute value of the difference between two successive approximations becomes very small compared with the values of x then again we can say that we have a good approximation to the root.  For example, as we try to locate the root of the function in the graph which happens to be between x = 1 and x = 2, if we notice that | x _n+1 - x _n | < 0.000001 * | x _n | and if our program has declared the values of x as float, then we can safely stop the iteration because there is no way we can further improve our estimate.

 When we start looking for a root, sometimes we know that the root must lie in a given interval.  We say that we have a bracket. Other times we only know that the root must be close to some given value, say x₀ . In this case we say that we have a good starting value. Some root finding methods require a bracket ( for example the bisection method), others require a good starting value ( for example Newton's method ).

How do we know a bracket or a good starting value for a root? This is a good question. Of course the easiest way to get this information is by plotting the function over the range of interest.  This we should do whenever we can.  Then we can approximately locate the root and use our methods to refine the estimate.  But we should mention that in cases where we need to solve single equations, whose behavior we can   visually investigate, we can use a plethora of software packages that will produce the root quickly and accurately ( for example MATLAB, Maple, Mathematica, MathCad, even Excel ).  The real challenge in root finding ( which requires use of a programming language ) is to write a procedure which will be able to locate the roots of many ( hundreds or thousands) equations, which are computer generated by a large code designed to solve a certain engineering problem.  In cases like these, it is obviously not possible to utilize human interaction in the solution process.  Generating good starting values and appropriate brackets in such cases requires a good understanding of the engineering problem at hand.