On-line Math 21

3.1  Trigonometric functions

Proof of the addition rule:

sin(A+B) = sin(A)cos(B)+cos(A)sin(B) cos(A+B) = cos(A)cos(B)-sin(A)sin(B)

We'll prove the second of these identities, by looking at a picture.

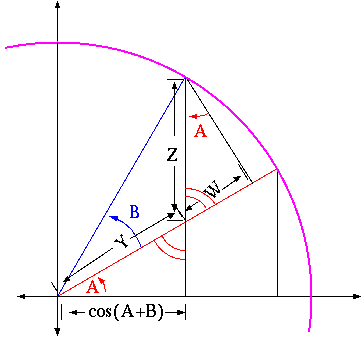
In this picture, the arc is an arc of the standard unit circle. Thus, the segment along the horizontal axis is, as indicated, cos(A+B) . Notice the marked pair of opposite angles. They are both of measure p/2-A , since the lower one is part of a right triangle with angle A . That implies that the other angle marked A is the same measure as the original A , again because of the right triangle (the sum of angles in a triangle is always p, and so the non-right angles of a right triangle add up to p/2 ).

By the definition of the cosine (the first definition), the distance Y satisfies

cos(A+B) Y = cos(A).

Look at the large right triangle with the angle B marked. Its base is Y+W , and its hypotenuse is 1 , so

Y+W = cos(B).

Also, the side opposite B has length sin(B) . Now look at the right triangle in the upper-right, with angle A . The side shared with the previous triangle is still sin(B) . That triangle implies that

W Z = sin(A), and also sin(B) Z = cos(A).

Thus,

W = Zsin(A) = sin(A)sin(B) cos(A) .

Previously, we had

Y = cos(A+B) cos(A) ,

and so, substituting in for Y and W ,

Y+W = cos(B) cos(A+B) cos(A) + sin(A)sin(B) cos(A) = cos(B).

Solving this last equation for cos(A+B) gives

cos(A+B) = cos(A)cos(B)-sin(A)sin(B),

which is just what we needed.

Now, this proof only holds for A and B positive, but it is easy to extend it to negative A and B , and to get the similar identity for cos(A-B) , by using cos(-x) = cos(x) and sin(-x) = -sin(x) .

I felt the need to prove one of these identities. They are in general not easy, but they do all follow from geometry, labelling everything carefully.

Copyright (c) by David L. Johnson, last modified
On 25 Apr 2000, 20:02..