Lehigh University
The Tribology Laboratory at Lehigh University
Research
Tribology
Wear of Materials
Wear is a complex process that occurs when two surfaces are slid against one another, resulting in gradual removal of one or both materials. The simple fact of wear is that it appears unavoidable, altering performance of mechanical and biological systems and ultimately resulting in system failure. Wear of materials is becoming increasingly important and could easily have as much of a functional and economic impact as friction. For example, in many industrial applications, components become worn and must be replaced. These replacements may be costly due to expensive components, labor and the down time of the equipment while the part is being replaced.
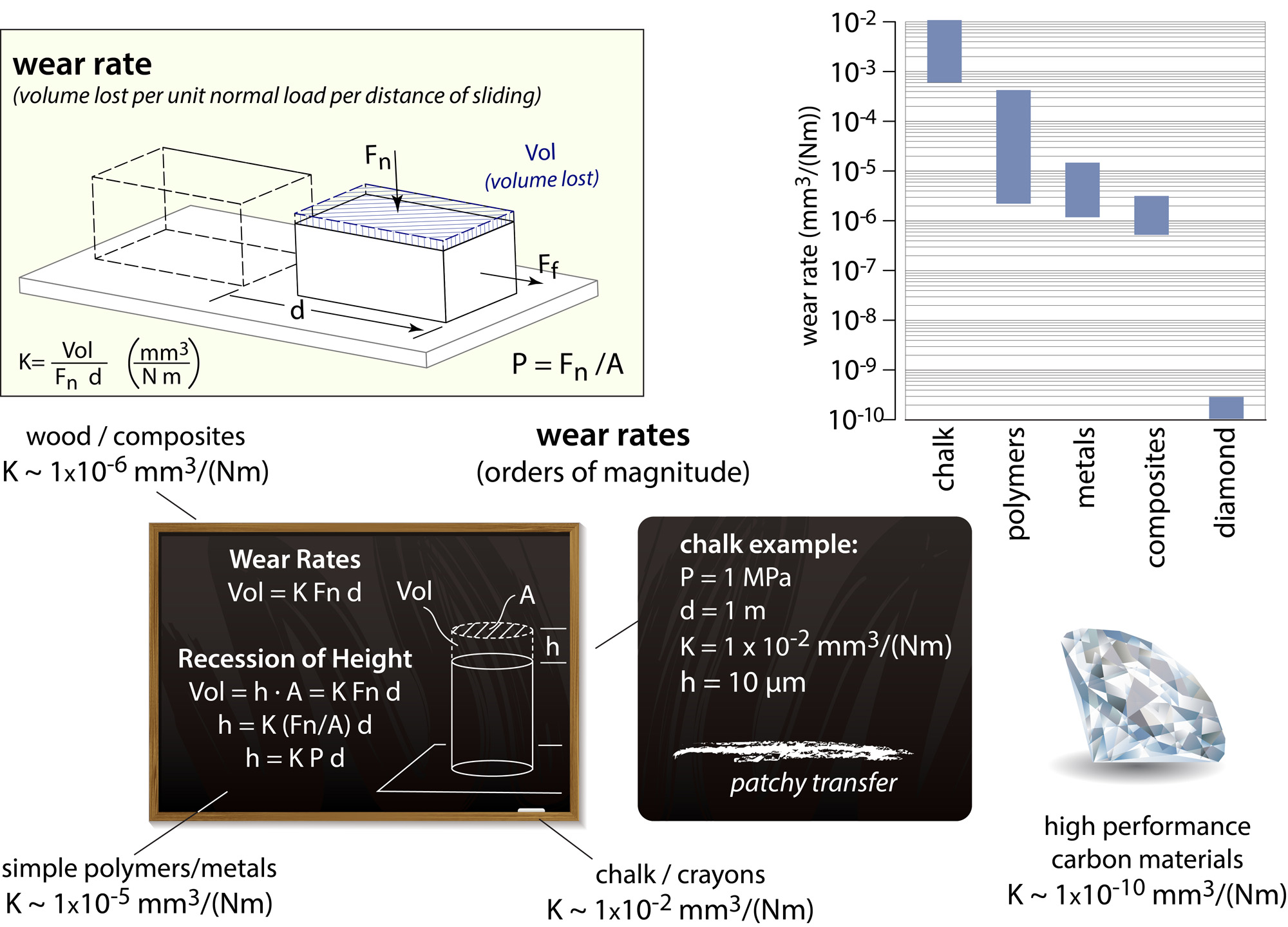
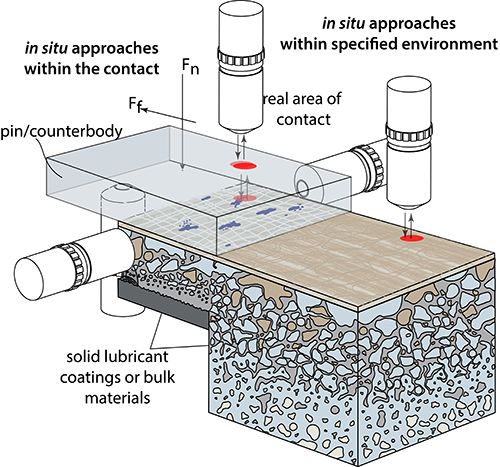
Studies of wear are of both fundamental and applied interests. One remarkable observation is that wear can vary more than eight orders of magnitude across material systems. It can vary several orders of magnitude for the same material just by changing the environment or the identity of the counter-material that the material is sliding against.
Mechanical engineers are trained to design around structural, thermal and even environmental failure criterion, so it is no surprise that many systems are sufficiently designed in these areas. The lack of knowledge on properly selecting materials for and designing tribological components combines with an underwhelming availability of low wear materials ultimately results in wear causing of end-of-useful-life and often catastrophic failure for many systems.
In fact, to paraphrase my advisor, wear is so commonly the end-of-useful-life for a design or product that the term “worn out” is synonymous with an acceptable end-of-useful-life of a product. The present global trend for efficiency, sustainability and the desire to push designs be faster and stronger, last longer and operate in extreme conditions has pushed the fundamental need for material development, specifically in the field of tribology, giving rise to the subfield of materials tribology.
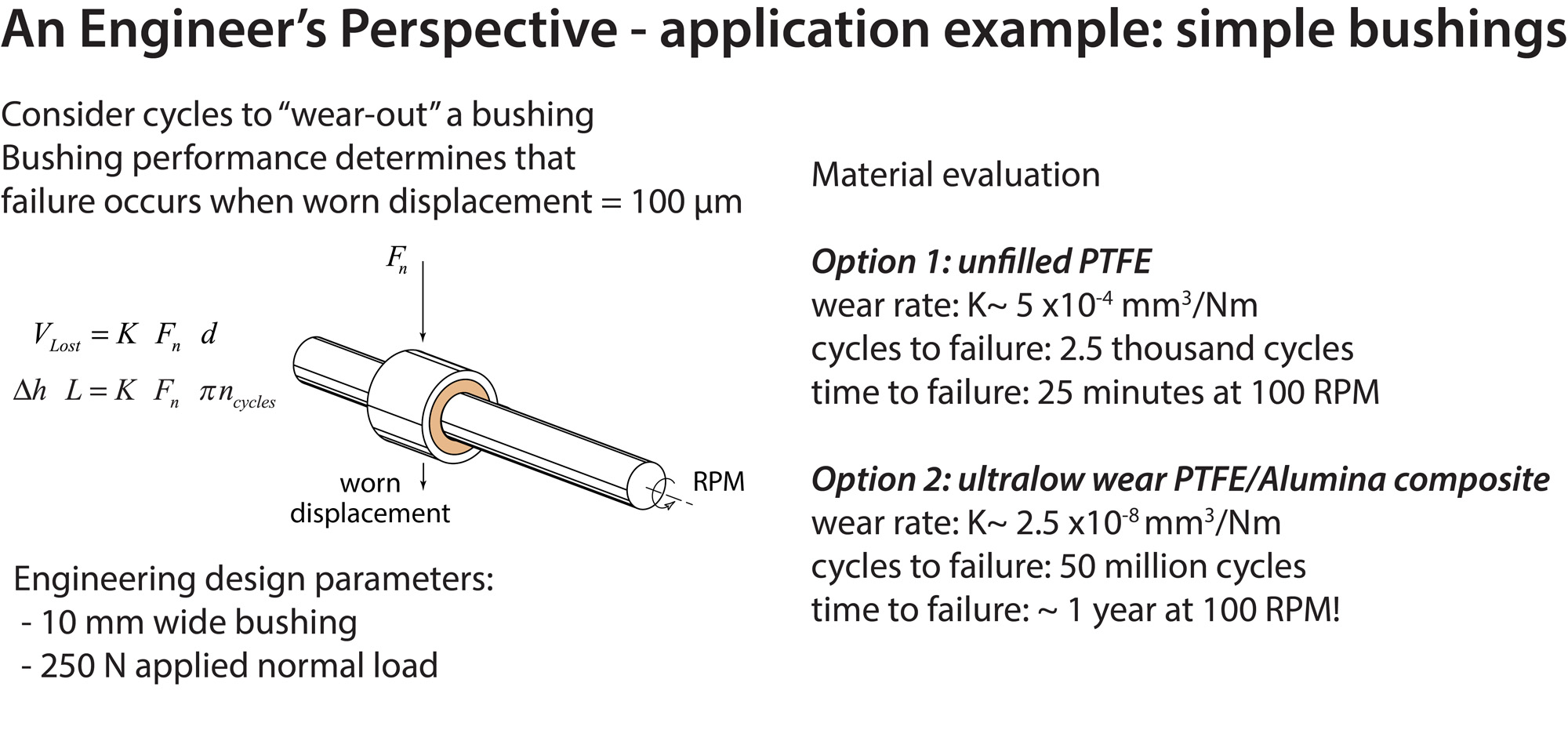
An accepted metric for reporting material wear was developed much later than for friction coefficient. Archard and Holm suggested that the total volume of material removed during sliding (the wear volume), V, is proportional to the real area of contact multiplied by the sliding distance by the unit-less proportionality constant known as a wear factor, K [1-3]. This wear factor can be a property of the material set, sliding conditions, surface topography and environment, among other things. The wear factor can be manipulated to calculate the often more convenient and more physically direct specific wear rate [4] (also known as a dimensional wear rate [5]), k, commonly measured in units of mm3/Nm . The specific wear rate is simply the wear volume divided by the product of the normal load and the sliding distance, d, as shown:
There are numerous methods for making volume loss measurements used to compute wear rates. These measurements can be made directly, or volume losses can be inferred based on:
- dimensional changes in the material including height changes
- topographical measurements of a wear made by a profilometer such as:
- optical measurements (microscope, SEM, etc.)
- interferometric measurement (interferometer)
- stylus profilometry
- atomic force microscopy
- interrupted mass measurements
- inferred measurements based on the running through of a coating by observation of an increased friction coefficient
Using the material density, a volume loss can be calculated by a change in mass. Wear rates are easily calculated by:
Schmitz et al., Colbert et al. and Burris and Sawyer provide modern uncertainty analyses to several of the methods used in this research to find wear rates [6-8].
1. Archard, J.F., Contact and rubbing of flat surfaces. Journal of Applied Physics, 1953. 24(8): p. 981-988.
2. Archard, J.F., Single contacts and multiple encounters. Journal of Applied Physics, 1961. 32(8): p. 1420-&.
3. Holm, R. and E. Holm, Electric contacts handbook. 1958, Berlin: Springer.
4. Stachowiak, G.W. and A.W. Batchelor, Engineering tribology. 2005, Oxford: Elsevier.
5. Williams, J.A., Engineering tribology. 1994, Oxford: Oxford University Press, Inc.
6. Schmitz, T.L., et al., The difficulty of measuring low friction: Uncertainty analysis for friction coefficient measurements. Journal of Tribology-Transactions of the Asme, 2005. 127(3): p. 673-678.
7. Burris, D.L. and W.G. Sawyer, Measurement uncertainties in wear rates. Tribology Letters, 2009. 36(1): p. 81-87.
8. Colbert, R.S. and W.G. Sawyer, Thermal dependence of the wear of molybdenum disulphide coatings. Wear, 2010. 269(11-12): p. 719-723.